一、時(shí)域與空域特性

以遠(yuǎn)場(chǎng)模型（平面波）為例，假設(shè)均勻線陣接收的為窄帶信號(hào)，假設(shè)相鄰振元間隔為d，入射角θ為：

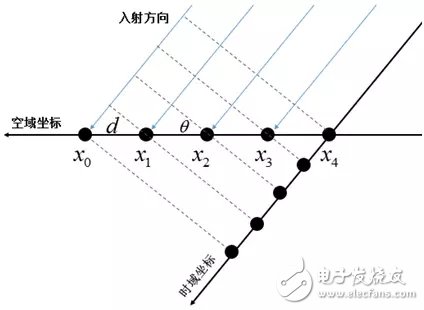
從空域坐標(biāo)來看，相鄰振元的間隔為：dsinθ

等價(jià)到時(shí)間軸來看，采樣點(diǎn)的間距為：dsinθ，對(duì)應(yīng)時(shí)間間隔為：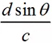

二、時(shí)、空域與采樣定理

A、空域角度理解

相鄰振元的相位差為：

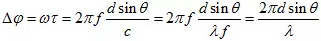
以干涉儀為例，如果存在相位模糊，有

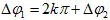
k為非零整數(shù)，如果希望不出現(xiàn)相位模糊

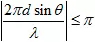
對(duì)應(yīng)掃描邊界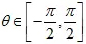，則有

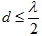
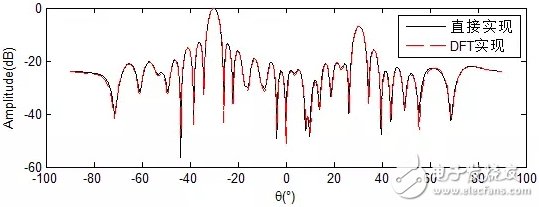
容易證明，同干涉儀一樣，均勻線陣譜估計(jì)中的導(dǎo)向矢量，如果不滿足上面的約束條件，同樣會(huì)有多峰的問題。

B、時(shí)域角度理解

前文提到，采樣點(diǎn)對(duì)應(yīng)的時(shí)間間隔為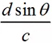，即采樣周期。空域均勻線陣對(duì)應(yīng)時(shí)域均勻采樣，采樣頻率：

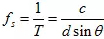
入射信號(hào)的頻率為：

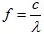
如果采樣無混疊，需要滿足Nyquist采樣定理：

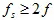
該約束條件等價(jià)于：

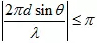
可以看出均勻線陣的相位無模糊對(duì)應(yīng)時(shí)域均勻采樣的奈奎斯特定理。多說一句，如果是非均勻線陣、圓陣等形式，可以理解成對(duì)應(yīng)維度的非均勻采樣；從空域角度理解，非均勻陣列可以解決模糊問題，從時(shí)域角度理解，稀疏采樣/非均勻采樣可以突破奈奎斯特采樣定理。

三、時(shí)、空域及功率譜

波束形成主要對(duì)感興趣的方向進(jìn)行增強(qiáng)/抑制，而譜估計(jì)更多是參數(shù)估計(jì)問題，前者操作多為主動(dòng)，后者操作多為被動(dòng)，MVDR算法對(duì)二者均適用。這里暫且拋開應(yīng)用場(chǎng)景，僅從時(shí)、空角度理解功率譜的”譜”特性。

接著上文的時(shí)域、空域思路，這里先從時(shí)域的角度來表述，為了簡(jiǎn)化均不考慮加窗情形。

A、時(shí)域角度理解

對(duì)于N點(diǎn)均勻采樣的信號(hào)uN(n)，對(duì)其進(jìn)行傅里葉變換：

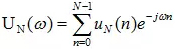
uN(n)的相關(guān)函數(shù)為：

容易證明有如下對(duì)應(yīng)關(guān)系：

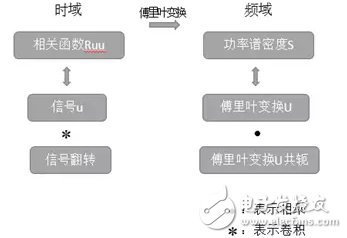
而相關(guān)函數(shù)對(duì)應(yīng)的傅里葉變換為功率譜密度，可以求解功率譜密度：

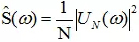
B、空域角度理解

N個(gè)均勻線陣接收單元，對(duì)應(yīng)的波束形成為：

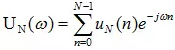
即空域的波束形成可以理解為時(shí)域的傅里葉變換，

從而空域的功率譜密度可以等價(jià)為：

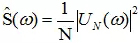
考慮到時(shí)域、空域具有等價(jià)性，空域的功率譜這么理解是合理的。

現(xiàn)在以常用的MVDR算法來理解這種等價(jià)性：

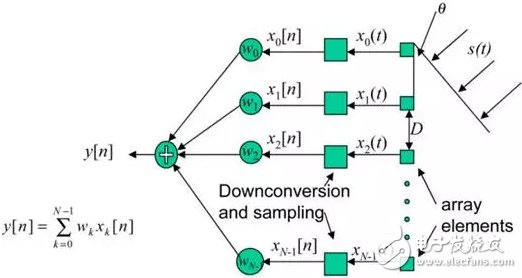
接收信號(hào)：

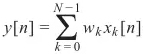
MVDR就是含有等式約束的最優(yōu)化問題：

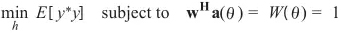
可以求解：

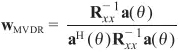
這個(gè)時(shí)候，如果將最優(yōu)的w帶入y，空域角度理解：y對(duì)應(yīng)就是波束形成的結(jié)果。時(shí)域角度理解：y對(duì)應(yīng)為傅里葉變換的結(jié)果。

通常MVDR的結(jié)果為E[y*y]的輸出，根據(jù)上文分析可知，該結(jié)果從時(shí)域理解就是功率譜（差一個(gè)常數(shù)），所以從空域角度稱作“譜”其實(shí)也是可以被接受的，對(duì)應(yīng)功率（譜）：

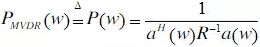
因?yàn)檫@是在空域，為了與時(shí)域功率譜的名字加以區(qū)別，可以稱其為空間譜。

具體空間譜名稱怎么由來，本文并沒有考證。本文只是提供了一種理解“空間譜”名稱的角度，至少M(fèi)USIC等算法的“譜”便與此不同，或許MUSIC等算法只是繼承了“空間譜”這個(gè)名詞也未可知。