前言

谷歌董事長施密特曾說過：雖然谷歌的無人駕駛汽車和機器人受到了許多媒體關(guān)注，但是這家公司真正的未來在于機器學習，一種讓計算機更聰明、更個性化的技術(shù)。

也許我們生活在人類歷史上最關(guān)鍵的時期：從使用大型計算機，到個人電腦，再到現(xiàn)在的云計算。關(guān)鍵的不是過去發(fā)生了什么，而是將來會有什么發(fā)生。

工具和技術(shù)的民主化，讓像我這樣的人對這個時期興奮不已。計算的蓬勃發(fā)展也是一樣。如今，作為一名數(shù)據(jù)科學家，用復雜的算法建立數(shù)據(jù)處理機器一小時能賺到好幾美金。但能做到這個程度可并不簡單！我也曾有過無數(shù)黑暗的日日夜夜。

誰能從這篇指南里受益最多？

我今天所給出的，也許是我這輩子寫下的最有價值的指南。

這篇指南的目的，是為那些有追求的數(shù)據(jù)科學家和機器學習狂熱者們，簡化學習旅途。這篇指南會讓你動手解決機器學習的問題，并從實踐中獲得真知。我提供的是幾個機器學習算法的高水平理解，以及運行這些算法的 R 和 Python 代碼。這些應該足以讓你親自試一試了。

我特地跳過了這些技術(shù)背后的數(shù)據(jù)，因為一開始你并不需要理解這些。如果你想從數(shù)據(jù)層面上理解這些算法，你應該去別處找找。但如果你想要在開始一個機器學習項目之前做些準備，你會喜歡這篇文章的。

廣義來說，有三種機器學習算法

1、監(jiān)督式學習

工作機制：這個算法由一個目標變量或結(jié)果變量（或因變量）組成。這些變量由已知的一系列預示變量（自變量）預測而來。利用這一系列變量，我們生成一個將輸入值映射到期望輸出值的函數(shù)。這個訓練過程會一直持續(xù)，直到模型在訓練數(shù)據(jù)上獲得期望的精確度。監(jiān)督式學習的例子有：回歸、決策樹、隨機森林、K – 近鄰算法、邏輯回歸等。

2、非監(jiān)督式學習

工作機制：在這個算法中，沒有任何目標變量或結(jié)果變量要預測或估計。這個算法用在不同的組內(nèi)聚類分析。這種分析方式被廣泛地用來細分客戶，根據(jù)干預的方式分為不同的用戶組。非監(jiān)督式學習的例子有：關(guān)聯(lián)算法和 K – 均值算法。

3、強化學習

工作機制：這個算法訓練機器進行決策。它是這樣工作的：機器被放在一個能讓它通過反復試錯來訓練自己的環(huán)境中。機器從過去的經(jīng)驗中進行學習，并且嘗試利用了解最透徹的知識作出精確的商業(yè)判斷。 強化學習的例子有馬爾可夫決策過程。

常見機器學習算法名單

這里是一個常用的機器學習算法名單。這些算法幾乎可以用在所有的數(shù)據(jù)問題上：

線性回歸

邏輯回歸

決策樹

SVM

樸素貝葉斯

K最近鄰算法

K均值算法

隨機森林算法

降維算法

Gradient Boost 和 Adaboost 算法

1、線性回歸

線性回歸通常用于根據(jù)連續(xù)變量估計實際數(shù)值（房價、呼叫次數(shù)、總銷售額等）。我們通過擬合最佳直線來建立自變量和因變量的關(guān)系。這條最佳直線叫做回歸線，并且用 Y= a *X + b 這條線性等式來表示。

理解線性回歸的最好辦法是回顧一下童年。假設(shè)在不問對方體重的情況下，讓一個五年級的孩子按體重從輕到重的順序?qū)Π嗌系耐瑢W排序，你覺得這個孩子會怎么做？他（她）很可能會目測人們的身高和體型，綜合這些可見的參數(shù)來排列他們。這是現(xiàn)實生活中使用線性回歸的例子。實際上，這個孩子發(fā)現(xiàn)了身高和體型與體重有一定的關(guān)系，這個關(guān)系看起來很像上面的等式。

在這個等式中：

Y：因變量

a：斜率

x：自變量

b ：截距

系數(shù) a 和 b 可以通過最小二乘法獲得。

參見下例。我們找出最佳擬合直線y=0.2811x+13.9。已知人的身高，我們可以通過這條等式求出體重。

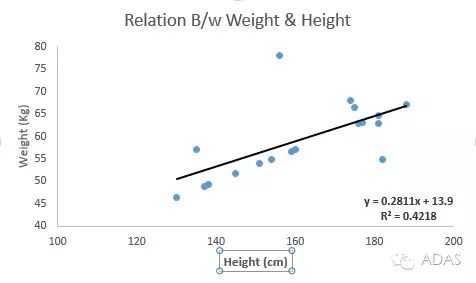
線性回歸的兩種主要類型是一元線性回歸和多元線性回歸。一元線性回歸的特點是只有一個自變量。多元線性回歸的特點正如其名，存在多個自變量。找最佳擬合直線的時候，你可以擬合到多項或者曲線回歸。這些就被叫做多項或曲線回歸。

Python 代碼(見原文)

2、邏輯回歸

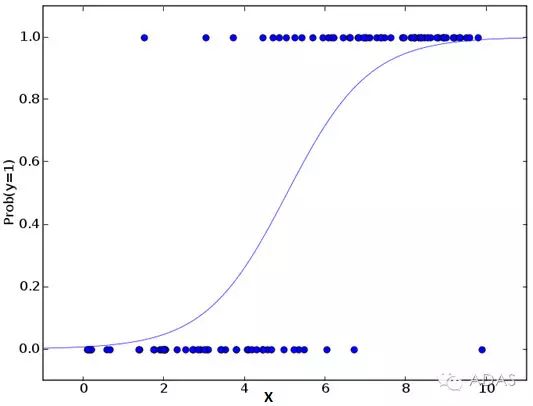
別被它的名字迷惑了！這是一個分類算法而不是一個回歸算法。該算法可根據(jù)已知的一系列因變量估計離散數(shù)值（比方說二進制數(shù)值 0 或 1 ，是或否，真或假）。簡單來說，它通過將數(shù)據(jù)擬合進一個邏輯函數(shù)來預估一個事件出現(xiàn)的概率。因此，它也被叫做邏輯回歸。因為它預估的是概率，所以它的輸出值大小在 0 和 1 之間（正如所預計的一樣）。

讓我們再次通過一個簡單的例子來理解這個算法。

假設(shè)你的朋友讓你解開一個謎題。這只會有兩個結(jié)果：你解開了或是你沒有解開。想象你要解答很多道題來找出你所擅長的主題。這個研究的結(jié)果就會像是這樣：假設(shè)題目是一道十年級的三角函數(shù)題，你有 70%的可能會解開這道題。然而，若題目是個五年級的歷史題，你只有30%的可能性回答正確。這就是邏輯回歸能提供給你的信息。

從數(shù)學上看，在結(jié)果中，幾率的對數(shù)使用的是預測變量的線性組合模型。

在上面的式子里，p 是我們感興趣的特征出現(xiàn)的概率。它選用使觀察樣本值的可能性最大化的值作為參數(shù)，而不是通過計算誤差平方和的最小值（就如一般的回歸分析用到的一樣）。

現(xiàn)在你也許要問了，為什么我們要求出對數(shù)呢？簡而言之，這種方法是復制一個階梯函數(shù)的最佳方法之一。我本可以更詳細地講述，但那就違背本篇指南的主旨了。

Python代碼(見原文)

更進一步：

你可以嘗試更多的方法來改進這個模型：

加入交互項

精簡模型特性

使用正則化方法

使用非線性模型

3、決策樹

這是我最喜愛也是最頻繁使用的算法之一。這個監(jiān)督式學習算法通常被用于分類問題。令人驚奇的是，它同時適用于分類變量和連續(xù)因變量。在這個算法中，我們將總體分成兩個或更多的同類群。這是根據(jù)最重要的屬性或者自變量來分成盡可能不同的組別。想要知道更多，可以閱讀：簡化決策樹。

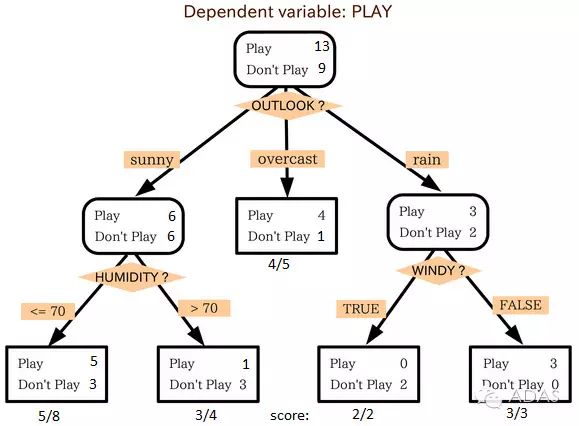
來源：statsexchange

在上圖中你可以看到，根據(jù)多種屬性，人群被分成了不同的四個小組，來判斷 “他們會不會去玩”。為了把總體分成不同組別，需要用到許多技術(shù)，比如說 Gini、Information Gain、Chi-square、entropy。

理解決策樹工作機制的最好方式是玩Jezzball，一個微軟的經(jīng)典游戲（見下圖）。這個游戲的最終目的，是在一個可以移動墻壁的房間里，通過造墻來分割出沒有小球的、盡量大的空間。

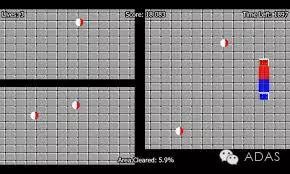
因此，每一次你用墻壁來分隔房間時，都是在嘗試著在同一間房里創(chuàng)建兩個不同的總體。相似地，決策樹也在把總體盡量分割到不同的組里去。

更多信息請見：決策樹算法的簡化

Python代碼(見原文)

4、支持向量機

這是一種分類方法。在這個算法中，我們將每個數(shù)據(jù)在N維空間中用點標出（N是你所有的特征總數(shù)），每個特征的值是一個坐標的值。

舉個例子，如果我們只有身高和頭發(fā)長度兩個特征，我們會在二維空間中標出這兩個變量，每個點有兩個坐標（這些坐標叫做支持向量）。

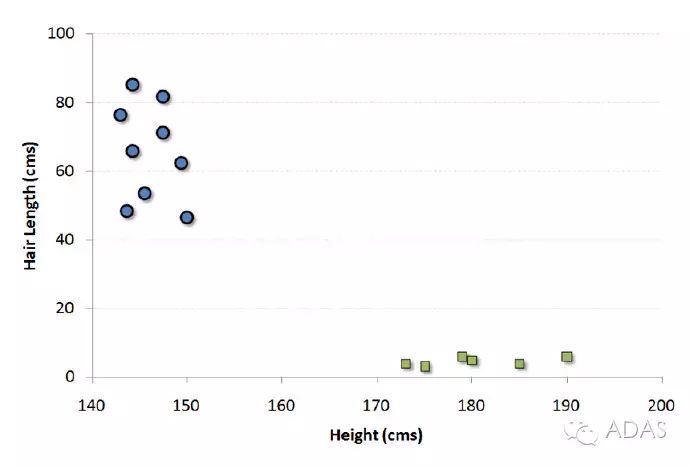
現(xiàn)在，我們會找到將兩組不同數(shù)據(jù)分開的一條直線。兩個分組中距離最近的兩個點到這條線的距離同時最優(yōu)化。

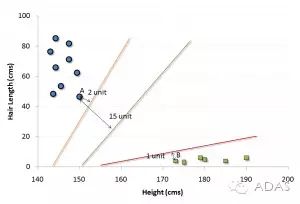
上面示例中的黑線將數(shù)據(jù)分類優(yōu)化成兩個小組，兩組中距離最近的點（圖中A、B點）到達黑線的距離滿足最優(yōu)條件。這條直線就是我們的分割線。接下來，測試數(shù)據(jù)落到直線的哪一邊，我們就將它分到哪一類去。

更多請見：支持向量機的簡化

將這個算法想作是在一個 N 維空間玩 JezzBall。需要對游戲做一些小變動：

比起之前只能在水平方向或者豎直方向畫直線，現(xiàn)在你可以在任意角度畫線或平面。

游戲的目的變成把不同顏色的球分割在不同的空間里。

球的位置不會改變。

Python代碼(見原文)

5、樸素貝葉斯

在預示變量間相互獨立的前提下，根據(jù)貝葉斯定理可以得到樸素貝葉斯這個分類方法。用更簡單的話來說，一個樸素貝葉斯分類器假設(shè)一個分類的特性與該分類的其它特性不相關(guān)。舉個例子，如果一個水果又圓又紅，并且直徑大約是 3 英寸，那么這個水果可能會是蘋果。即便這些特性互相依賴，或者依賴于別的特性的存在，樸素貝葉斯分類器還是會假設(shè)這些特性分別獨立地暗示這個水果是個蘋果。

樸素貝葉斯模型易于建造，且對于大型數(shù)據(jù)集非常有用。雖然簡單，但是樸素貝葉斯的表現(xiàn)卻超越了非常復雜的分類方法。

貝葉斯定理提供了一種從P(c)、P(x)和P(x|c) 計算后驗概率 P(c|x) 的方法。請看以下等式：

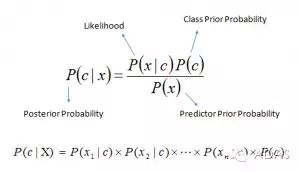
在這里，

P(c|x) 是已知預示變量（屬性）的前提下，類（目標）的后驗概率

P(c)是類的先驗概率

P(x|c)是可能性，即已知類的前提下，預示變量的概率

P(x)是預示變量的先驗概率

例子：讓我們用一個例子來理解這個概念。在下面，我有一個天氣的訓練集和對應的目標變量“Play”。現(xiàn)在，我們需要根據(jù)天氣情況，將會“玩”和“不玩”的參與者進行分類。讓我們執(zhí)行以下步驟。

步驟1：把數(shù)據(jù)集轉(zhuǎn)換成頻率表。

步驟2：利用類似“當Overcast可能性為0.29時，玩耍的可能性為0.64”這樣的概率，創(chuàng)造 Likelihood 表格。

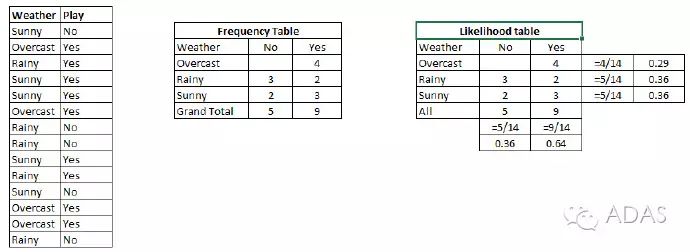
步驟3：現(xiàn)在，使用樸素貝葉斯等式來計算每一類的后驗概率。后驗概率最大的類就是預測的結(jié)果。

問題：如果天氣晴朗，參與者就能玩耍。這個陳述正確嗎？

我們可以使用討論過的方法解決這個問題。于是 P（會玩 | 晴朗）= P（晴朗 | 會玩）* P（會玩）/ P （晴朗）

我們有 P （晴朗 |會玩）= 3/9 = 0.33，P（晴朗） = 5/14 = 0.36, P（會玩）= 9/14 = 0.64

現(xiàn)在，P(會玩 | 晴朗）= 0.33 * 0.64 / 0.36 = 0.60，有更大的概率。

樸素貝葉斯使用了一個相似的方法，通過不同屬性來預測不同類別的概率。這個算法通常被用于文本分類，以及涉及到多個類的問題。

Python代碼(見原文)

6、KNN（K – 最近鄰算法）

該算法可用于分類問題和回歸問題。然而，在業(yè)界內(nèi)，K – 最近鄰算法更常用于分類問題。K – 最近鄰算法是一個簡單的算法。它儲存所有的案例，通過周圍k個案例中的大多數(shù)情況劃分新的案例。根據(jù)一個距離函數(shù)，新案例會被分配到它的 K 個近鄰中最普遍的類別中去。

這些距離函數(shù)可以是歐式距離、曼哈頓距離、明式距離或者是漢明距離。前三個距離函數(shù)用于連續(xù)函數(shù)，第四個函數(shù)（漢明函數(shù)）則被用于分類變量。如果 K=1，新案例就直接被分到離其最近的案例所屬的類別中。有時候，使用 KNN 建模時，選擇 K 的取值是一個挑戰(zhàn)。

更多信息：K – 最近鄰算法入門（簡化版）

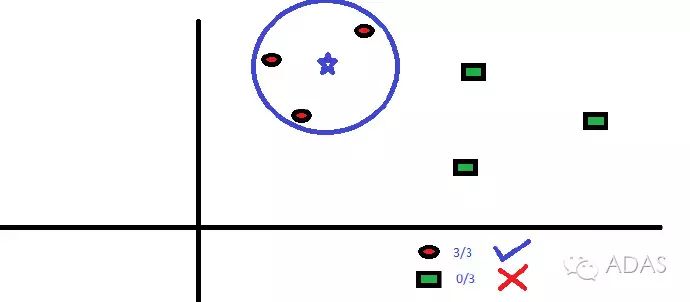
我們可以很容易地在現(xiàn)實生活中應用到 KNN。如果想要了解一個完全陌生的人，你也許想要去找他的好朋友們或者他的圈子來獲得他的信息。

在選擇使用 KNN 之前，你需要考慮的事情：

KNN 的計算成本很高。

變量應該先標準化（normalized），不然會被更高范圍的變量偏倚。

在使用KNN之前，要在野值去除和噪音去除等前期處理多花功夫。

Python代碼(見原文)

7、K 均值算法

K – 均值算法是一種非監(jiān)督式學習算法，它能解決聚類問題。使用 K – 均值算法來將一個數(shù)據(jù)歸入一定數(shù)量的集群（假設(shè)有 k 個集群）的過程是簡單的。一個集群內(nèi)的數(shù)據(jù)點是均勻齊次的，并且異于別的集群。

還記得從墨水漬里找出形狀的活動嗎？K – 均值算法在某方面類似于這個活動。觀察形狀，并延伸想象來找出到底有多少種集群或者總體。

K – 均值算法怎樣形成集群：

K – 均值算法給每個集群選擇k個點。這些點稱作為質(zhì)心。

每一個數(shù)據(jù)點與距離最近的質(zhì)心形成一個集群，也就是 k 個集群。

根據(jù)現(xiàn)有的類別成員，找出每個類別的質(zhì)心。現(xiàn)在我們有了新質(zhì)心。

當我們有新質(zhì)心后，重復步驟 2 和步驟 3。找到距離每個數(shù)據(jù)點最近的質(zhì)心，并與新的k集群聯(lián)系起來。重復這個過程，直到數(shù)據(jù)都收斂了，也就是當質(zhì)心不再改變。

如何決定 K 值：

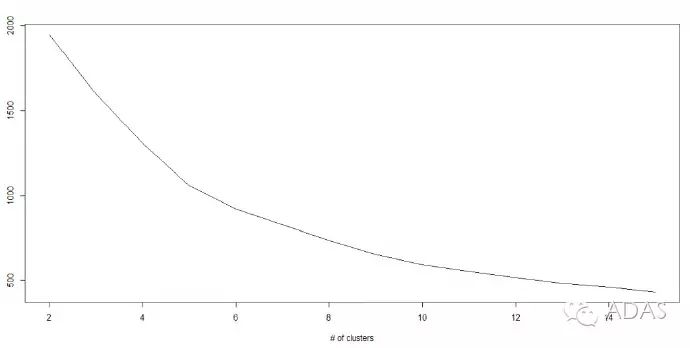
K – 均值算法涉及到集群，每個集群有自己的質(zhì)心。一個集群內(nèi)的質(zhì)心和各數(shù)據(jù)點之間距離的平方和形成了這個集群的平方值之和。同時，當所有集群的平方值之和加起來的時候，就組成了集群方案的平方值之和。

我們知道，當集群的數(shù)量增加時，K值會持續(xù)下降。但是，如果你將結(jié)果用圖表來表示，你會看到距離的平方總和快速減少。到某個值 k 之后，減少的速度就大大下降了。在此，我們可以找到集群數(shù)量的最優(yōu)值。

Python代碼(見原文)

8、隨機森林

隨機森林是表示決策樹總體的一個專有名詞。在隨機森林算法中，我們有一系列的決策樹（因此又名“森林”）。為了根據(jù)一個新對象的屬性將其分類，每一個決策樹有一個分類，稱之為這個決策樹“投票”給該分類。這個森林選擇獲得森林里（在所有樹中）獲得票數(shù)最多的分類。

每棵樹是像這樣種植養(yǎng)成的：

如果訓練集的案例數(shù)是 N，則從 N 個案例中用重置抽樣法隨機抽取樣本。這個樣本將作為“養(yǎng)育”樹的訓練集。

假如有 M 個輸入變量，則定義一個數(shù)字 m<

盡可能大地種植每一棵樹，全程不剪枝。

若想了解這個算法的更多細節(jié)，比較決策樹以及優(yōu)化模型參數(shù)，我建議你閱讀以下文章：

隨機森林入門—簡化版

將 CART 模型與隨機森林比較（上）

將隨機森林與 CART 模型比較（下）

調(diào)整你的隨機森林模型參數(shù)

Python(見原文)

9、降維算法

在過去的 4 到 5 年里，在每一個可能的階段，信息捕捉都呈指數(shù)增長。公司、政府機構(gòu)、研究組織在應對著新資源以外，還捕捉詳盡的信息。

舉個例子：電子商務(wù)公司更詳細地捕捉關(guān)于顧客的資料：個人信息、網(wǎng)絡(luò)瀏覽記錄、他們的喜惡、購買記錄、反饋以及別的許多信息，比你身邊的雜貨店售貨員更加關(guān)注你。

作為一個數(shù)據(jù)科學家，我們提供的數(shù)據(jù)包含許多特點。這聽起來給建立一個經(jīng)得起考研的模型提供了很好材料，但有一個挑戰(zhàn)：如何從 1000 或者 2000 里分辨出最重要的變量呢？在這種情況下，降維算法和別的一些算法（比如決策樹、隨機森林、PCA、因子分析）幫助我們根據(jù)相關(guān)矩陣，缺失的值的比例和別的要素來找出這些重要變量。

想要知道更多關(guān)于該算法的信息，可以閱讀《降維算法的初學者指南》。

Python代碼(見原文)

10、Gradient Boosting和AdaBoost 算法

當我們要處理很多數(shù)據(jù)來做一個有高預測能力的預測時，我們會用到 GBM 和 AdaBoost 這兩種 boosting 算法。boosting 算法是一種集成學習算法。它結(jié)合了建立在多個基礎(chǔ)估計值基礎(chǔ)上的預測結(jié)果，來增進單個估計值的可靠程度。這些 boosting 算法通常在數(shù)據(jù)科學比賽如 Kaggl、AV Hackathon、CrowdAnalytix 中很有效。

更多：詳盡了解 Gradient 和 AdaBoost

Python代碼(見原文)

GradientBoostingClassifier 和隨機森林是兩種不同的 boosting 樹分類器。人們常常問起這兩個算法之間的區(qū)別。

結(jié)語

現(xiàn)在我能確定，你對常用的機器學習算法應該有了大致的了解。寫這篇文章并提供 Python 和 R 語言代碼的唯一目的，就是讓你立馬開始學習。如果你想要掌握機器學習，那就立刻開始吧。做做練習，理性地認識整個過程，應用這些代碼，并感受樂趣吧！

原文標題：10 種機器學習算法的要點（附 Python 和 R 代碼）

文章出處：【微信公眾號：ADAS】歡迎添加關(guān)注！文章轉(zhuǎn)載請注明出處。