無線傳感器網絡的許多應用要求節點知道自身的位置信息，才能向用戶提供有用的檢測服務。沒有節點位置信息的監測數據在很多場合下是沒有意義的。比如，對于森林火災檢測、天然氣管道監測等應用，當有事件發生時，人們關心的一個首要問題就是事件發生在哪里，此時如果只知道發生了火災卻不知道火災具體的發生地點，這種監測沒有任何實質的意義，因此節點的位置信息對于很多場合是至關重要的。

在許多場合下，傳感器節點被隨機部署在某個區域，節點事先無法知道自身的位置，因此需要在部署后通過定位技術來獲取自身的位置信息。目前最常見的定位技術就是GPS（Global Positioning System）了，它能夠通過衛星對節點進行定位，并且能夠達到比較高的精度。因此要想對傳感器節點進行定位，最容易想到的方法就是給每個節點配備一個GPS接收器，但是這種方法不適用于傳感器網絡，主要原因有以下幾點：

1）GPS接收器通常能耗高，而對于無線傳感器網絡中的節點來說，一般能耗很有限，給每個節點配備一個GPS接收器會大大縮短網絡壽命；

2）GPS接收器成本比較高，給無線傳感器網絡中的每個節點配備一個GPS接收器，需要投入很大成本，尤其對于大規模的無線傳感器網絡來說不是很適合；

因此有必要研究適合無線傳感器網絡的定位技術。下面分兩個部分來介紹節點定位的相關研究：1）節點定位的基本概念；2）節點定位的基本思路；3）常見算法。

一.節點定位的基本概念

無線傳感器網絡中的節點定位是指傳感器節點根據網絡中少數已知節點的位置信息，通過一定的定位技術確定網絡中其他節點的位置信息的過程。

在無線傳感器網絡中節點通常可以分為信標節點（beacon node or anchor node）和未知節點（unknown node），其中信標節點也稱為錨節點或者參考點，未知節點也稱為普通節點。信標節點是位置信息已知的節點，未知節點是未知信息未知的節點。信標節點一般所占比例很小，通常通過手工配置或者配備GPS接收器來獲取自身的位置信息。

除此之外還有一種節點稱為鄰居節點（neighbor node），鄰居節點是指傳感器節點通信半徑內的其他節點。

以下是幾個常用術語：

到達時間（Time of Arrvial，TOA），信號從一個節點傳播到另一個節點所需時間

到達時間差（Time Diffrential of Arrival，TDOA），不同傳播速度的信號從一個節點到達另一個基點所需要的時間之差

到達角度（Angle of Arrival，AOA），節點接收到的信號相對于自身軸線的角度

接收信號強度（Received Sinnal Strength，RSS），節點接收到無限信號強度的大小，也有稱Received Sinnal Strength Indicator（RRSI），兩個意思基本是一樣的

視距關系（Light of Sight，LOS），兩個節點之間沒有障礙物，能夠直接通信

非視距關系（Non Light of Sight，NLOS），兩個節點之間有障礙物，不能直接通信

跳數（Hop Count），兩個節點之間的跳段之和

二.節點定位技術的基本思路

節點定位的基本思路主要有兩種：

1.基于測距（Range-based）：假設在傳感器網絡中某些節點位置信息已知，通過某些手段來估算其他節點的位置信息。在這里面通常有兩個步驟：

測距

位置估算

因為要通過信標節點得到未知節點的位置信息，必須先確定信標節點到未知節點的距離，才能得到未知節點的位置信息。舉個例子說明一下：

假如信標節點A位置已知為（x1，y1），節點M位置未知，要想求得M的位置，最簡單的想法：假設B位置為（x，y），A到B的距離為d1，則有

d12=（x-x1）2+（y-y1）2

顯然只根據一個方程這樣是無法求得x和y的值，假若有兩個信標節點呢？

這樣一來的話又多了一個方程：d22=（x-x2）2+（y-y2）2，此時可以解得方程組得到x和y，但是此時x和y是有兩組解的，無法唯一確定x和y的值，因此需要考慮再假如一個信標節點：

這樣一來的話就可以唯一確定x和y的值了，最基本的定位思想就是這樣。這里舉的例子是采用距離，還可以采用角度。

一般情況最少需要知道未知節點和信標節點的三組距離或角度值，然后再通過位置估算方法確定位置。

通常測距的方法有4種：

1）基于到達時間（TOA）的測距

這種方法是根據已知信號的傳播速度及信號在發送節點和接收節點之間的傳播時間來估算距離，這種方法要求能夠非常精確地獲取發送節點和接收節點之間的傳播時延，這個是比較困難的，難度很大，不太適合無線傳感器網絡。

2）基于到達時間差（TDOA）的測距

這種方法中發送節點同時發送兩種不同傳播速度的信號、接收節點根據兩種信號到達的時間差和他們的傳播速度來計算距離。假若兩種信號的傳寶速度為v1和v2，到達時間分別為t1和t2，發送節點到接收節點的距離為d，則有：

t1-t2=d/v1-d/v2

可得d=（t1-t2）v1v2/（v2-v1）

3）基于到達角度（AOA）的測距

這種方法根據接收信號到達時候與自身軸線的角度來計算，這種方法對硬件成本要求很高，要求配備天線陣列，不太適合無線傳感器網絡

4）基于接收信號強度（RSS）的測距

信號在傳播過程中會有衰減，無線信號的發射功率和接收功率存在某種映射關系，因此可以利用關系這個來估算距離，

在獲得了距離之后，就可以來估算位置了，常用的位置估算方法有下面兩種：

1）三邊測量法

上面舉的例子中的位置估算方法就是三邊測量法，此處不再贅述。

至于某些文獻上提到的三角測量法個人覺得跟三邊測量法是一回事，就不再介紹了。

3）最大似然估計法

已知n個節點的坐標為（x1，y1），（x2，y2）......（xn，yn），它們到未知節點M的距離分別為d1，d2......dn，則有：

（x-x1）2+（y-y1）2=d12

（x-x2）2+（y-y2）2=d22

......

（x-xn）2+（y-yn）2=dn2

依次用第一個方程減去最后一個方程，可得：

x12-xn2+y12-yn2+dn2-d12=2x(x1-xn)+2y(y1-yn)

......

xn-12-xn2+yn-12+dn2-dn-12=2x(xn-1-xn)+2y(yn-1-yn)

則可以表示成?AX?=?B

其中A =?

B=

X =（x,y)T

2.無需測距（range-free）

無需測距的方法一般是利用網絡連通性或者拓撲結構來估算距離，再利用三邊測量法或者極大似然估計來估算位置。

三.常見算法

1.基于測距（range-based）

1）AHLos 算法?

該算法是基于到達時間差的測距，信標節點首先向鄰居節點以兩種射頻信號來廣播消息，然后鄰居節點根據到達時間差來估算距離，在接收到三個信標節點的消息之后，則根據三邊測量法估算位置，鄰居節點確定自己的位置之后轉變為信標節點，也向鄰近節點廣播消息重復上述過程直至所有節點定位完成。

2）RADAR算法

該算法是基于RSS的測距，而基于RSS測距該算法有兩種模型：經驗模型和信號傳播模型

先說一下經驗模型：

在經驗模型中，節點被分散在一定的區域內，并且保證所有的未知節點能夠與信標節點直接通信，如圖所示。然后事先在該區域內采集一些位置進行RSS強度測試，并以（x，y，RSS）的形式記錄到數據庫中。當進行定位時，未知節點同數據庫中的數據進行比對，選擇差值最小的三個或者三個以上點作為估算位置，然后再采用三邊測量法或者下文的質心法來估算位置。

信號傳播模型：

信號傳播模型主要有兩種模型：自由空間模型和shadowing模型

自由空間模型假定信號發射功率和信號接收功率存在確定的映射關系：?

其中PR是接收處的功率，PS是發射處的功率，d是發射點距接收點的距離，α是傳播因子，視環境而定。

shadowing模型：

其中P（d）是未知節點處的信號強度或者信號發射功率，P（d0）是距信標節點或者基站d0處的信號發射功率（其中d0是參考距離，一般取1m），n是衰減因子，由于實際環境中存在噪聲，所以引入了?，比如在室內傳播，會有墻壁或者門這些障礙物，就需要計算?。

2.無需測距（range-free）

無需測距的定位算法不需要直接測量節點之間的距離或者角度，而是根據網絡的連通性來實現位置估計得，典型的無需測距的算法主要有以下幾種：

1）質心算法

質心算法基于兩個假設條件：射頻信號的傳播遵循理想的圓球模型；節點的通信半徑相同且不會改變。

該算法利用了計算幾何中質心的思想，假設n邊形的頂點坐標分別為（x1，y1）......（xn，yn），設其質心坐標為（x，y），則有

x=（x1+x2....+xn）/ n

y=（y1+y2+....+yn）/ n

算法核心思想為：信標節點周期性地廣播包含自身位置信息的消息，在時間t內未知節點收到來自信標節點i的消息數目為Nr（i，t），而時間t內信標節點i發出的消息數目為Ns（i，t），那么未知節點和信標節點的連通指標為：

C=Nr（i，t）/ Ns（i，t）

如果C大于設定的閾值，則認為未知節點處于信標節點i的覆蓋區域內，即與信標節點i連通。這樣對于每個未知節點都可以選出與其連通的所有信標節點，然后把這些信標節點的質心作為該未知節點的坐標。

質心算法是一種完全基于網絡連通性的定位算法，其計算和實施難度都比較小，但是算法精度不高，并且通常要求信標節點具有較高的密度。

2）DV-HOP（Distance Vector-Hop）算法

DV-HOP算法是為了避免對節點距離直接測量而提出的一種基于矢量路由的非測距定位算法。該算法的核心思想是通過距離矢量路由方法獲取未知節點與信標節點之間的最小跳數，并計算每跳的平均距離，然后以每跳的平均距離與最小跳數的乘積作為未知節點與信標節點的估算距離，再使用三邊測量法估算未知節點的坐標位置。舉個例子：

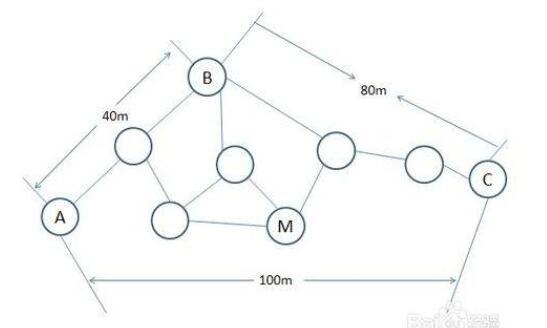
A、B、C為信標節點，M為未知節點，A到B和C的距離分別為40m和100m，而A到B和C的最小跳數分別為2和5，則A的平均跳距為：

（40+100）/ （2+5）=20m，同理可以得到B和C的平均跳數為24m和22.5m，則可以計算M距離三個信標節點的距離分別為：

3*20m，2*24m，3*22.5m，然后就可以利用三邊測量法估算出M的坐標。這種方法實現比較簡單，但是精度較差，不適合稀疏的以及拓撲不規則的網絡。

3）APIT算法

APIT算法的基本思想同質心算法的思想類似，它利用由信標節點組成的三角形覆蓋重疊區域來確定未知節點的位置。在APIT算法中，未知節點首先在其鄰居節點中收集信標節點的信息。然后任意選取3個信標節點，判斷自己是否在這3個信標節點組成的三角形區域內，然后不斷這樣循環選取3個信標節點進行判斷，這樣，未知節點可以確定多個包含自己的三角形區域，這些三角形區域的重疊部分是一個多邊形，它確定了更小的包含未知節點的區域，然后以這個多邊形區域的質心作為未知節點的坐標。

4）MAP算法

MAP（Mobile Anchor Point）是一種基于移動信標節點的非測距定位算法，也有稱為MAN（Mobile Anchor Node）。其基本思想是利用可移動的信標節點在監測區域中移動并周期性的廣播其當前的位置信息，然后可以確定兩條以未知節點為圓心的弦，這兩條弦的垂直平分線的交點就是圓心。

如圖所示，S為未知節點，M為移動的信標節點，在T1時刻M移動到S的通信范圍之內，然后在T5時刻移出S的通信范圍，這樣就可以確定了兩條弦 ?T1T5，在T12時刻M又重新移動到S的通信范圍之內，然后又在T15時刻移出S的通信范圍，這樣又可以確定一條弦T12T15，這兩條弦的垂直平分線的交點即為圓心S的坐標，然后以圓心坐標作為未知節點S的位置。

該算法有與其他非測距定位算法相比有較高的精確度，但是缺點是移動節點是必須要有足夠能量支持其在監測區域內移動，并且當未知節點的位置發生變化時，該算法有比較大的誤差。

5）Amorphous算法

Amorphous算法與DV-HOP算法類似，其分為三個階段：

第一階段：計算未知節點與每個信標節點之間的最小跳數

第二階段：假設網絡中的節點通信半徑相同，并且每跳的平均距離等于節點的通信半徑，計算未知節點到每個信標節點的距離

第三階段：采用三邊測量法或者最大似然估計法估算未知節點的位置

6）凸規劃定位算法

凸規劃定位算法的核心思想是：如果兩個節點能夠直接進行通信，則它們之間的距離必定小于節點的通信半徑。

如圖所示，黑色實心點為信標節點，白色空心點為未知節點，假若未知節點能與信標節點通信，則其必在以信標節點為圓心、通信半徑為半徑的圓內，這樣的話，多個這樣的圓的相交區域必然包含了未知節點，然后以相交區域構成的矩形的質心作為未知節點的坐標。

7）Ring-Overlapping算法

該算法利用交疊環的思想進行定位，比如S為未知節點，A、B、C為信標節點，若A發出射頻信號，而S處的信號強度RSS小于B處的信號強度而大于C處的信號強度，則S必在以A-B為內半徑、A-C為外半徑的環形區域內，類似地分別可以得到以B、C為中心的環形區域，而S必在這些環形區域的交疊區域內，然后以交疊區域的質心作為S的坐標。

以上算法都是有信標節點的定位算法，曾有人提出了一些沒有信標節點的定位算法如SPA（Self-positioning Algorithm）算法，這種算法主要是建立全局坐標系來估算未知節點的位置，但是這種算法復雜度非常高，不適合用于大規模網絡，也有人提出針對SPA算法的改進算法，如SDGPSN（Scalable and Distributed GPS free Positioning for?Sensor Networks）算法。

還有一部分人提出了一些其他的算法，比如AFL（Anchor-Free Distributed Localization in Sensor Networks）算法，其利用的是局部估算方法。還有人提出了基于分簇的定位算法（Using Clustering Information for Sensor?Network Localization）。

定位算法暫時就介紹這么多了，相關深入內容將在后面繼續講解。