由一位全加器(FA)構成的行波進位加法器，它可以實現補碼數的加法運算和減法運算。但是這種加法/減法器存在兩個問題：一是由于串行進位，它的運算時間很長。假如加法器由n位全加器構成，每一位的進位延遲時間為20ns，那么最壞情況下， 進位信號從最低位傳遞到最高位而最后輸出穩定，至少需要n*20ns，這在高速計算中顯然是不利的。二是就行波進位加法器本身來說，它只能完成加法和減法兩種操作而不能完成邏輯操作。本節我們介紹的多功能算術/邏輯運算單元(ALU)不僅具有多種算術運算和邏輯運算的功能，而且具有先行進位邏輯， 從而能實現高速運算。
　　
　　1.基本思想
　　
　　一位全加器(FA)的邏輯表達式為
　　
　　F_i＝A_i⊕B_i⊕C_i　　
　　C_i＋1＝A_iB_i＋B_iC_i＋C_iA_i???????? (2.35)
　　
　　我們將A_i和B_i先組合成由控制參數S₀，S₁，S₂，S₃控制的組合函數X_i和Y_i，然后再將Xi，Yi和下一位進位數通過全加器進行全加。這樣，不同的控制參數可以得到不同的組合函數，因而能夠實現多種算術運算和邏輯運算。

圖2.10　ALU的邏輯結構原理框圖

　　因此，一位算術/邏輯運算單元的邏輯表達式為
　　
　　F_i=X_i⊕Y_i⊕X_n+i　　
　　C_n+i+1=X_iY_i+Y_iC_n+i+C_n+iX_i
　　
　　上式中進位下標用n＋i代替原來以為全加器中的i，i代表集成在一片電路上的ALU的二進制位數。對于4位一片的ALU，i＝0，1，2，3。n代表若干片ALU組成更大字長的運算器時每片電路的進位輸入，例如當4片組成16位字長的運算器時，n＝0，4，8，12。

2.邏輯表達式
　　
　　控制參數S₀，S₁，S₂，S₃ 分別控制輸入A_i 和B_i ，產生Y和X的函數。其中Y_i是受S₀ ，S₁控制的A_i和B_i的組合函數，而X_i是受S₂，S₃控制的A_i和B_i組合函數，其函數關系如表2.4所示。

表2.4 X_i，Y_i與控制參數和輸入量的關系

　　根據上面所列的函數關系，即可列出Xi和Yi的邏輯表達式
　　
　　X_i＝S₂S₃＋S₂S₃（A_i＋B_i）＋S₂S₃（A_i＋B_i）＋S₂S₃A_i　　
　　Y_i＝S₀S₁A_i＋S₀S₁A_iB_i＋S₀S₁A_iB_i

　　進一步化簡并代入前面的求和與進位表達式，可得ALU的某一位邏輯表達式如下

??? ?　?(2.36)

4位之間采用先行進位公式，根據式（2.36），每一位的進位公式可遞推如下：
　　
　　第0位向第1位的進位公式為
　　
　　C_n＋1＝Y₀＋X₀C_n
　　
　　其中C_n是向第0位（末位）的進位。
　　
　　第1位向第2位的進位公式為
　　
　　C_n＋2＝Y₁＋X₁C_n＋1＝Y₁＋Y₀X₁＋X₀X₁C_n
　　
　　第2位向第3位的進位公式為
　　
　　C_n＋3＝Y₂＋X₂C_n＋2＝Y₂＋Y₁X₂＋Y₀X₁X₂＋X₀X₁X₂C_n
　　
　　第3位的進位輸出（即整個4位運算進位輸出）公式為
　　
　　C_n＋4＝Y₃＋X₃C_n＋3＝Y₃＋Y₂X₃＋Y₁X₂X₃＋Y₀X₁X₂X₃＋X₀X₁X₂X₃C_n
　　
　　設

　　G＝Y₃＋Y₂X₃＋Y₁X₂X₃＋Y₀X₁X₂X₃
　　P＝X₀X₁X₂X₃
　　
　　則
　　
　　C_n＋4＝G＋PC_n???????????? (2.37)
　　
　　這樣，對一片ALU來說，可有三個進位輸出。其中G稱為進位發生輸出，P稱為進位傳送輸出。在電路中多加這兩個進位輸出的目的，是為了便于實現多片（組）ALU之間的先行進位，為此還需一個配合電路，稱之為先行進位發生器(CLA)，下面還要介紹。

C_n+4是本片(組)的最后進位輸出。邏輯表達式表明，這是一個先行進位邏輯。換句話說，第0位的進位輸入C_n可以直接傳送到最高位上去，因而可以實現高速運算。
　　
　　用正邏輯表示的4位算術/邏輯運算單元(ALU)的邏輯電路圖如下，它是根據上面的原始推導公式用TTL電路實現的。這個器件的商業標號為74181ALU。

?

3.算術邏輯運算的實現
　　
　　上演示圖中除了S₀－S₃四個控制端外，還有一個控制端Ｍ，它使用來控制ALU是進行算術運算還是進行邏輯運算的。
　　
　　當Ｍ＝0時，Ｍ對進位信號沒有任何影響。此時F 不僅與本位的被操作數Y和操作數X 有關，而且與本位的進位輸出，即C 有關，因此Ｍ＝0時，進行算術操作。
　　
　　當Ｍ＝1時，封鎖了各位的進位輸出，即C ＝0，因此各位的運算結果F 僅與Y 和X 有關，故Ｍ＝1時，進行邏輯操作。
　　
　　圖2.11(b)示出了工作于負邏輯和正邏輯操作數方式的74181ALU方框圖。顯然，這個器件執行的正邏輯輸入/輸出方式的一組算術運算和邏輯操作與負邏輯輸入/輸出方式的一組算術運算和邏輯操作是等效的。

圖2.11 74181ALU的邏輯電路圖和方框圖

表2.5列出了74181ALU的運算功能表，它有兩種工作方式。對正邏輯操作數來說，算術運算稱高電平操作，邏輯運算稱正邏輯操作(即高電平為“1”，低電平為“0”)。對于負邏輯操作數來說，正好相反。由于S －S 有16種狀態組合，因此對正邏輯輸入與輸出而言，有16種算術運算功能和16種邏輯運算功能。同樣，對于負邏輯輸入與輸出而言，也有16種算術運算功能和16種邏輯運算功能。

表2.5 74181ALU算術/邏輯運算功能表

　　說明：(1)H＝高電平，L＝低電平.(2)*表示每一位均移到下一個更高位，即A*＝2A
　　
　　注意，表2.5中算術運算操作是用補碼表示法來表示的。其中“加”是指算術加，運算時要考慮進位，而符號“＋”是指“邏輯加”。其次，減法是用補碼方法進行的，其中數的反碼是內部產生的，而結果輸出“A減B減1”，因此做減法時需在最末位產生一個強迫進位(加1)，以便產生“A減B”的結果。另外，“A＝B”輸出端可指示兩個數相等，因此它與其他ALU的“A＝B”輸出端按“與”邏輯連接后，可以檢測兩個數的相等條件。

4.兩級先行進位的ALU
　　
　　前面說過，74181ALU設置了P和G兩個本組先行進位輸出端。如果將四片74181的P，G輸出端送入到74182先行進位部件（CLA），又可實現第二級的先行進位，即組與組之間的先行進位。
　　
　　假設4片（組）74181的先行進位輸出依次為P₀，G₀，G₁P₁，P₂，G₂，P₃，G₃，那么參考式(2.37)的進位邏輯表達式，先行進位部件74182CLA所提供的進位邏輯關系如下：
　　
　　C_n＋ｘ＝G₀＋P₀C_n　　
　　C_n＋ｙ＝G₁＋P₁C_n＋ｘ＝G₁＋G₀P₁＋P₀P₁C_n　
　　C_n＋ｚ＝G₂＋P₂C_n＋ｙ＝G₂＋G₁P₂＋G₀P₁P₂＋P₀P₁P₂C_n　　　　　　(2.38)　
　　C_n＋4 ＝G₃＋P₃C_n＋ｚ＝G₃＋G₂P₃＋G₁P₁P₂＋G₀P₁P₂P₃＋P₀P₁P₂P₃C_n
　????? 　＝G*＋P*C_n
　　
　　其中
　　
　　P*＝P₀P₁P₂P₃　
　　G*＝G₃＋G₂P₃＋G₁P₁P₂＋G₀P₁P₂P₃
　　
　　根據以上表達式，用TTL器件實現的成組先行進位部件74182的邏輯電路圖如下所示，其中G*稱為成組進位發生輸出，P*稱為成組進位傳送輸出。

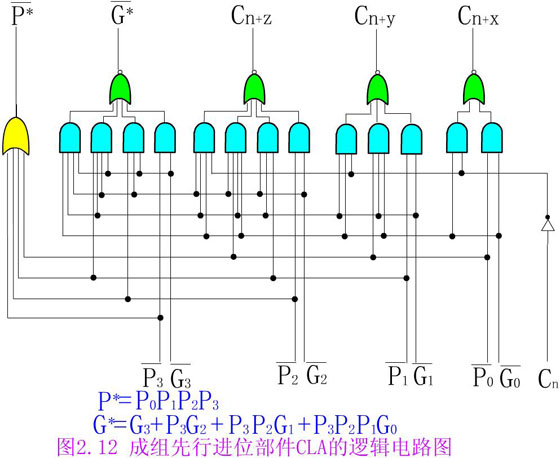
下面介紹如何用若干個74181ALU位片，與配套的74182先行進位部件CLA在一起，構成一個全字長的ALU。
　　
　　下圖示出了用兩個16位全先行進位部件級聯組成的32位ALU邏輯方框圖。在這個電路中使用了八個74181ALU和兩個74182CLA器件。很顯然，對一個16位來說，CLA部件構成了第二級的先行進位邏輯，即實現四個小組（位片）之間的先行進位，從而使全字長ALU的運算時間大大縮短。

　　圖2.13　用兩個6位全先行進位部件級聯組成的32位ALU