數字設計基礎知識--頻率與時間
在低頻時,一段普通導線可以有效地將兩個電路短接在一起,但在調頻時就不同了。高頻狀態下,只有寬的,扁平的,導體才能夠有效地短接兩個電路。同樣一段導線,在低頻時有效的,但在調頻狀態下因電感太大而無法完成短接功能。我們可以把它用做一個調頻電感,而不是一個調頻短接電路。
這是一個普遍現象嗎?難道在某個頻率范圍工作正常的電路元件在另一個頻率范圍就無法工作嗎?電氣參數對頻率真的如此敏感嗎?
的確如此,如果以對數頻率為一個坐標軸,幾乎沒有哪個電氣參數在超過10個或20個十倍頻程的范圍內依然能夠保持為常數。因此,對于每個電氣參數,我們必須考慮其有效的頻率范圍。
為了進一步闡明這個極寬的頻段范圍概念,首先來考慮對應極長時間周期的一個極低頻率,隨后將討論在極高頻率時的情況。
一個10的-12次方HZ的正弦波每30000年才完成一個周期。TTL(晶體管-晶體管邏輯)電平的10的-12次方HZ正弦波平均每天中相應的變化值比1UV還小。這的確是一個非常低的頻率,但并不等于零。
有關半導體10的-12HZ頻率的任何實驗,最后都不可能實現。完成10的-12次方HZ頻率的實驗所需的時間實在是太長,以致于電路已經化為灰燼了,在這樣長的時間段內觀察,集成電路只是一小塊氧化硅而已。
當我們把頻率急劇提高時,時間周期會變得非常短,那此電氣參數也會發生變化。例如在1KHZ時,一段短的接在導線經測量得到的電阻為0.01歐,而在1GHZ時,由于趨膚效應,電阻增加到1.0歐,不僅如此,還得到了50歐的感抗。
當頻率上升至電路元件工作頻率范圍的上限時,元件性能常常會發生較大的變化。
多高的頻率范圍對于高速數字設計才重要呢?圖1.1回答了這個問題,圖中描述了一個隨機數字脈沖序列與其頻譜的重要部分之間的關系。

圖1.1所示的數字信號是由一個D型觸發器輸出的,其時鐘頻率為F。在每個時鐘周期,數據的值在1和0之間隨機地觸發。在這個例子中,10~90%上升和下降時間記為T,為時鐘周期的1%。
如圖1.1所示,這一信號的頻譜功率密謀在時鐘頻率的各個倍頻上顯示為空,而且從F向上直到標記為F的頻率點,總的斜率為-20DB/DECADE。超過F,頻譜滾降則大大快于20DB/十倍頻程。而在轉折頻率點F,頻譜功率的幅值比按20DB/十倍頻程滾降的預期值低了一半。對于任何數字信號,轉折頻率與其數字邊沿的上升(和下降)時間有關,而與它的時鐘速率無關:

其中,F=轉折頻率,數字脈沖的大部分能量集中在該頻率以下T=脈沖上升時間。
縮短上升時間會提高F頻率。拉長上升時間則會降低F頻率。
任何數字信號的重要時域特性主要由F頻率以下的信號頻譜所決定,從這一法則我們可以定性地推導出數字電路的兩個重要特性:
1、任何在其F頻率以內具有一個平坦頻率響應的電路,可以允許一個數字信號幾乎無失真地通過。
2、數字電路在F頻率以上的頻率特性對于它如何處理數字信號幾乎沒有影響。
注意:F只由信號上升時間定義,而且與其他頻域參數沒有直接參與聯系。這個簡明的定義使得F容易使用,而且容易記憶。
當使用F的時候,應該記信這是一種不精確的頻譜測量方法。作為一個參考標志,F能幫助我們把頻率影響的結果區分為完全無關緊要的、或者僅僅是令人不安的以及完全破壞性的等幾個級別。在大多數數字問題中,這正是我們所希望的知道的。
當然,F也有局限性,F不能精確地預測系統的工作情況,甚至也不能精確地定義如何測量上升時間!F不能代替已經成熟的傅里葉分析方法,也不能用來預測電磁輻射。電磁輻射的特性取決于F頻率以上部分的具體頻譜的情況。
同時,對于數字信號,F能夠以實用而有效的方式迅速地將時間和頻率聯系起來。我們將在本書中通篇使用F作為數字信號所含頻譜成分的實際上邊界。
加到前述推導的特性1,如果系統在F之下的頻率范圍內有一個非平坦的頻率響應,那么它是如何使數字信號產生畸變的呢?這里有一個例子。
我們知道,一個電路的調頻響應影響它對瞬時過程的處理(比如上升時間)。電路的低頻響應影響它對長期過程的處理。圖1.2說明了一個電路在調頻和低頻時具有不同特性。這個電路可以通過調頻變化,但是不能通過低頻變化(長期的穩定部分)。
讓我們從一個特定頻率F開始分析圖1.2。在頻率F,電容C具有一電抗(也就是阻抗的大小)為(C2πF)

我們用這個公式計算電抗議并且用上升時間替換F:

其中,TR=階躍輸入的上升時間,S
????? F=階躍輸入的最高頻率,HZ
?????
????? C=電容,F
式中顯示了如何用轉折頻率或上升時間來估算一個電容的電抗。
在圖1.2的電路中,一個0.6歐的電抗實際起一個短接的作用。全振幅的脈沖前沿將直接沖過這個電容。
時間間隔超過25NS,容性電抗增加到15歐,導致耦合信號的幅度顯著下降。
本文地址:http://www.solar-ruike.com.cn/article/88/131/189/2010/20100528218628.html
 電子發燒友App
電子發燒友App










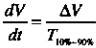












評論