REACTIVE POWER OPTIMIZATION OF POWER SYSTEM BASED ON MODIFIED?
SIMULATED ANNEALING ALGORITHM

Jia Dexiang1 Tang Guoqing1 Han Jing2

(1. Dept. of Electrical Engineering, Southeast University, Nanjing 210096;?
2. Maanshan Electric Power Supply Bureau, Maanshan 243000)

　　Abstract: The key to the optimization of reactive power operation is to get optimum value or satisfying quasi optimum value. Traditional linear programming technique and non-linear programming technique can not deal with the problem of integer variable successfully, and the simulated annealing algorithm(SA) is not very robust. Allowing for the characteristics of high-medium voltage distribution system, the SA is modified as follows: using remembrance-guided search method, and modifying the quasi optimum value by pattern search. Numerical experiment demonstrates that, the above method is reasonable, feasible, and practical to some extent.
　　Key words: reactive power optimization; remembrance-guided search; pattern search method; modified simulated annealing algorithm

0．引言
　　無功運行優化（RPOP）問題一直受到人們的重視，因為我國的線損率歷來居高不下。例如，2001年安徽省總發電量約為400億千瓦·時，電網的實際統計線損率約為20％，即線損電量約為80億千瓦·時，其中可變線損電量約為60億千瓦·時[1]。農網損耗甚至高達28％[2]。網損的嚴重性由此可見一斑。在現有電網結構的基礎上，通過合理調節無功潮流可以降低網損、提高電壓質量和電網運行的經濟性。無功運行優化問題是一個大規模非線性整數規劃問題。其目標通常為網損最小，也有采用偏移量最小，控制設備調節量最小或操作設備次數最少等作為目標函數。其等約束條件一般為各節點功率平衡，不等約束條件包括節點電壓、線路功率和各控制量調節范圍的限制[3]。其算法主要有線性規劃法，非線性規劃法，混合整數規劃法，動態規劃法，人工智能法等，目前還沒有一種方法能保證求出無功優化問題的最優解[4]。
　　對于110KV-35KV高中壓配電網，其調節無功潮流的主要手段是改變有載調壓變壓器的分接頭位置和并聯電容器的投切組數，這些控制變量一般為整型。傳統的線性規劃法和非線性規劃法等先將這些整型控制量視為連續變量，待求出最優解后再取近似的整數值，誤差較大；或者采用分支定界求解，計算時間過長。近年來，許多學者采用人工智能法求解RPOP問題。文獻5采用遺傳算法結合神經網絡預算電網潮流，減少了大規模電網遺傳算法的整體計算時間。文獻6采用記憶指導的模擬退火方案，較好地實現了配電網電容器的三相分相優化投切問題。
　　模擬退火法（Simulated Annealing，簡稱SA）具有隨機尋優的特點，能較好地避免局部極值點的束縛。但是SA求解速度慢，魯棒性不強。因此，本文采用改進模擬退火算法（ISA）求解RPOP問題。主要改進點如下：采用記憶指導搜索方法，加快了搜索速度；采用模式法局部尋優，增加了獲得全局最優解的可能性。數值對比試驗表明，上述改進方法是合理的和可行的。

1 數學模型
　　高中壓配電網無功運行優化的主要目的就是在滿足各種約束條件下，通過改變有載調壓變壓器的分接頭位置和并聯電容器的投切組數，使有功網損最小。其數學模型為：
　
　　其中，控制量u包括電網中發電機或可連續調整無功補償設備的無功出力，有載調壓變壓器的分接頭檔位和并聯電容器投入運行的組數；狀態量x包括各節點的電壓模值和相角。
　　等約束條件為基本潮流方程組，即各節點有功功率和無功功率平衡，包括負荷功率與網損之和等于發電功率。
　　不等約束條件數量較多，主要包括：節點電壓模值的上下限約束，線路和變壓器通過的最大功率約束，有載調壓變壓器變比調整范圍的約束，有功電源出力上下限的約束，可調無功電源出力上下限的約束[3]。其中，有載調壓變壓器的分接頭檔位和并聯電容器投運的組數均取整數。
　　在SA中，不等約束條件通常作為懲罰項附加在目標函數上。本文采用的目標函數為：Ps(u,x)+cK。其中Ps(u,x)為有功網損，K為違反不等約束條件的次數，c為懲罰因子。對于不同類型的不等約束條件，懲罰因子c可取不同數值。當約束條件比較重要時，如電壓越上限（大于1.1倍的額定電壓）和線路功率越限等，c可取1；當約束條件不太重要時，如電壓越下限（小于0.95倍但是大于0.9倍的額定電壓）等，c可取0.5。

2 算法
　　SA是1953年Metropolis等人提出的。它模擬物理學中固體物質（如金屬）的退火過程來求解組合優化問題。在物理退火過程中，通常先將金屬加熱至熔化，使其中的粒子可以自由移動，即處于高能態。然后逐漸降低溫度，使粒子形成低能態的晶格。只要在凝固點附近溫度下降得足夠慢，物質就能擺脫局部應力的束縛，形成最低能量的基態－晶體[7]。將晶體與最優值、冷卻過程與尋優過程對應起來，從而形成SA算法。SA求解步驟如下[8]：
　　1）從可行解空間中任選一初始狀態x0，計算其目標函數值f(x0)，并選擇初始控制溫度T0和馬爾可夫鏈（Markov Chain）的長度。
　　2）在可行解空間中產生一個隨機擾動，得到新狀態x1, 計算其目標函數值f(x1)。
　　3）判斷是否接收：如果f(x1)< f(x0)，則接受新狀態x1為當前狀態。否則按Metropolis準則判決是否接受x1，若接受，則令當前狀態等于x1；若不接受，則令當前狀態等于x0。
　　4）根據某個收斂準則，判斷抽樣過程是否終止，是則轉5，否則轉2。
　　5）按照某個溫度冷卻方案降低控制溫度T。
　　6）根據某個收斂準則，判斷退火過程是否終止，是則轉7，否則轉2。
　　7）以當前解作為最優解輸出。
　　SA能以足夠高的概率（接近1）收斂于全局最優點，其前提是：初始溫度足夠高，溫度下降足夠慢和終止溫度足夠低。實際應用中很難滿足這些要求，因而其求解結果不太理想。另外SA搜索效率較低，最后輸出的結果可能比中間結果差。多年來，SA的主要改進之處在于初始溫度的選擇、降溫策略和終止判據上。初始溫度一般取與目標函數同一數量級的某個數值。在鄰域搜索過程中，當解的質量變差的概率呈Boltzmann分布時，S. Geman和D. Geman證明了按T=T0/log(1+t)降溫策略可使SA搜索到全局最優，其中t為降溫次數[9]。在搜索后期，當解的質量變差的概率呈Cahchy分布時，H. Szu和R. Hartley提出了按T=T0/(1+t)的快速降溫策略可使SA搜索到全局最優[10]，從而盡量避免了搜索在全局最優解的鄰域內波動。終止判據也有多種取法，例如取控制溫度下降到某一設定的最低溫度、當前最優值經歷的Markov Chain個數等。
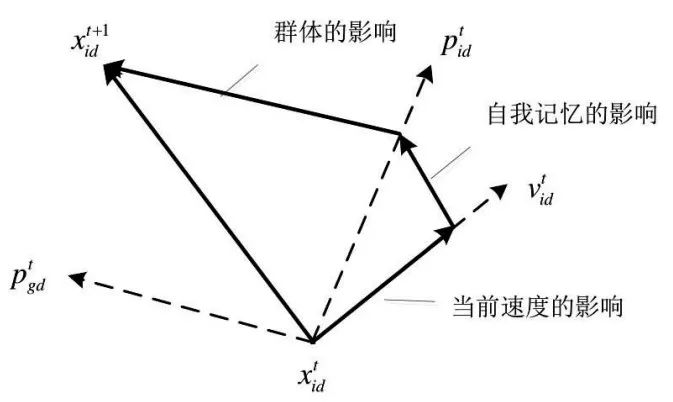
　　考慮到計算的復雜度以及可編程性，本文采用記憶指導搜索方法結合模式法局部尋優，來求解RPOP問題。所謂記憶指導，是指取前一階段（即記憶長度）搜索結果中的最優值作為下一階段搜索的起點，這種方法在一定程度上避免了搜索的盲目性。局部尋優能力較差幾乎是所有隨機搜索方法的通病，而模式法（Pattern Search，簡稱PS）比較適合局部尋優，因此本文采用模式法對每個鏈中的最優值進行局部尋優，并采用整個搜索結果中的最優值作為輸出結果，從而增加了獲得全局最優解的可能性。終止判據取最低控制溫度和最優值保留鏈數相結合的方式。
　　PS是1961年 Hooke和Jeeves提出的一種直接求解優化問題方法。PS的長處在于能夠追尋谷線（脊線）加速移向最優解[11]。本文運用PS對SA的每個鏈中的最優值進行局部尋優，具體步驟是：取每個鏈中的最優點作為初始基點B1；確定各獨立控制變量Ui的步長；依次對Ui的兩個方向進行攝動，并按目標函數值優化的方向移動矢點；當所有變量都被攝動后，即可得到新基點B2；從B1+2(B2-B1)點開始進行類似的攝動，就得到了新基點B3；再從B2+2(B3-B2)點開始重復上述步驟進行探索和加速，直到目標函數值不再下降，局部尋優迭代終止。PS提高了SA的局部尋優能力。

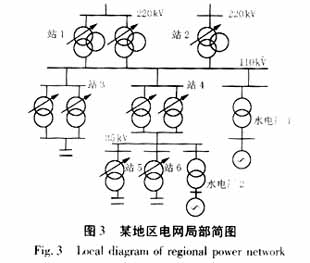
3 算例
　　本文以IEEE－30節點系統的無功優化問題為例，對所提的算法進行驗證。IEEE－30節點系統的數據見文獻12。該系統包括6臺發電機、4臺變壓器和2套并聯電容器。設控制變量為4臺變壓器，2套并聯電容器。為了突出高中壓配電網的特點，便于分析和比較，發電機的無功發電量未作控制量。設線路變壓器變比可調，變比上下限分別為1.1和0.9，其分級步長為2.5%，分接頭檔位變量設為整型，其取值范圍是[-4，4]。設節點24電容器分為2組，投切組數變量設為整型，其取值范圍是[0，2]。節點10電容器分為大小相等的4組 ，投切組數變量設為整型，其取值范圍是[0，4]。功率基準值為100MVA。SA的初始溫度T0取10，降溫策略采用T=kT0的簡化方式，其中溫度衰減系數k取較大值（0.95），這樣雖然導致迭代次數的增加，但能搜索更大范圍的解空間，有利于獲取全局最優解。馬爾可夫鏈長取得較短（50），以便減少算法時間。擾動量的產生方法是：在每一個整型控制分量的取值序列中分別按1/3概率上下移動一位或不作移動。對于惡化解點x，按概率exp((f(x')-f(x))/T)進行接受，其中x'為前次解點，f(x')和f(x)為相應解點的目標函數值。PS局部尋優的初始步長取1。終止判據取最小控制溫度0.05或最優值保留鏈數40。記憶尋優的長度取10。由于PS與初始值的選取關系密切，且易于陷入局部極值點，而SA初期的目標函數值一般偏大，為了加快計算速度，當溫度下降到1以下才開始對每個鏈中的最優個體進行局部尋優。
　　考慮到無功優化的計算時耗主要在于求解潮流方程組上，隨著電網規模的擴大，SA本身所耗時間相差不大，所以本文僅從求解潮流方程組的次數和最優值的分布兩方面進行比較。在上述假設條件下，無功優化的精確解為7.05014MW，為了求得此解，共需要對94*5*3 ＝ 98415個潮流方程組進行計算。下表為幾種SA改進方法的對比試驗數據，每種方法共進行了20次試驗，表中按序號所列的每種方法都是在前一種方法基礎上增加的改進點。

　　上表說明，每增加一種改進措施，都改善了解點的質量以及收斂的穩定性。其中，記憶最優值方式明顯縮短了解點與全局最優點之間的距離。而組合終止判據顯著減少了迭代求解潮流方程組的次數，加快了計算速度，其缺點是解點的質量稍有惡化。記憶指導搜索進一步加快了計算速度，并提高了解的質量。PS局部尋優對于獲得高質量的解點特別有效，在PS局部尋優的20次試驗中，有11次收斂于全局最優點，另外9次收斂點略次于全局最優點，其缺點是求解潮流方程組的次數增加了10.5%，但試驗效果還是令人滿意的。

4 結論
　　本文運用改進模擬退火算法(ISA)求解高中壓配電網的無功優化問題，能夠以較大概率獲得全局最優解，收斂的穩定性較好。仿真試驗驗證了本文所述方法是合理的和可行的。試驗發現，ISA求解RPOP問題，還存在著如下問題：
　　1）．降溫策略的確定。雖然都是依據大范圍粗略搜索、小范圍精確搜索的原則，但是不同的降溫策略對于整體計算速度和最終解的質量影響較大。對于不同的優化問題，往往需要經過多次試驗才能找到較為合適的降溫策略。
　　2）．局部尋優方法的改進。本文所做的試驗中，局部尋優平均要解782次潮流方程組，占總次數的19.56%，這也是影響求解速度的主要因素之一。
　　這些問題將是本文的后續研究點，歡迎各位專家和學者給予指導。