王鵬飛,蔣坤,張峰(陸軍炮兵防空兵學院,合肥 230031)
摘 要
高超聲速飛行器因其重要的戰略地位已經成為各國爭奪空天權所關注的焦點。控制系統設計是保證高超聲速飛行器實用化的關鍵技術。針對吸氣式高超聲速飛行器,設計一種反步控制器。為增強反步控制器的魯棒性,引入徑向基神經網絡對高超聲速飛行器縱向非仿射動力學模型中的不確定函數進行在線逼近。為了解決輸入受限帶來的控制問題,構造一種新型輔助系統對跟蹤誤差和控制律進行補償,實現在控制輸入瞬時飽和情況下的穩定跟蹤。最后,基于MATLAB仿真驗證了控制策略的有效性。
1 引 言
隨著人類對太空的探索日益增多,臨近空間(距水平面20~100 km)因其特殊的空間位置受到人們越來越多的關注[1]。高超聲速飛行器作為一種能夠飛行在臨近空間的新型飛行器,正成為各軍事大國爭相發展的目標。由于高超聲速飛行器的動力學特性呈現出顯著的非線性和非最小相位特點,因此給其控制系統的設計帶來了巨大挑戰。目前,以反步控制、滑模控制、智能控制等為代表的非線性控制已逐漸成為高超聲速飛行器控制系統設計的主流方法。反步控制形成于20世紀90年代,它體現了一種層疊設計思想,即通過遞歸構造閉環系統的Lyapunov函數,從而保證閉環系統軌跡的有界性和收斂性。反步控制的缺點是存在虛擬控制量導數反復求導導致的“微分膨脹”問題[2-5]。
孟堯等[4]采用動態面技術避免了對虛擬控制變量的重復求導。文獻[5]通過滑模微分器獲取虛擬控制量的導數,從而避免了“微分膨脹”問題。滑模控制也稱為變結構控制,它能夠使得系統按照預定的“滑動模態”的狀態軌跡運動。由于“滑動模態”與對象參數無關,因此滑模控制具有響應速度快、魯棒性強等特點,但是其缺點是抖振現象較為嚴重,容易激發飛行器的彈性振動[6-9]。黃書童等[8]利用雙冪次趨近律代替原有符號函數,設計了一種雙冪次滑模反步控制策略,降低了抖振的影響。
文成馀等[9] 將控制律內的符號函數連續化,設計了一種快速平滑的二階滑模控制系統。智能控制常用來處理復雜不確定性系統,主要包括神經網絡控制和模糊控制等[10-12]。相較傳統控制方法,智能控制不依賴于精確模型,因而具有更強的自適應和魯棒性。
文獻[13]將高超聲速飛行器的軌跡跟蹤轉化為對角速率誤差的最優控制,利用神經網絡逼近最優控制中的代價函數,從而獲得最優的反饋控制律。張迎雪等[14]針對高超聲速飛行器的快/慢回路分別設計了分數階比例、積分和微分(Proportional Integral Derivative,PID)控制器,利用模糊控制的任意逼近性在線調節PID參數,顯著提升了控制系統的魯棒性。高超聲速飛行器獨特的動力學特性要求其本身的執行機構必須受限,即輸入受限問題。吳立剛等[15]討論了受限條件下滑模面的最大收斂域問題。
文獻[16]針對輸入受限時控制系統的穩定性無法保證的問題,引入輔助系統對跟蹤誤差進行補償,保證了在出現執行機構飽和時控制系統對參考軌跡的穩定跟蹤。綜合前面的研究成果,本文針對高超聲速飛行器輸入受限問題,提出一種反步神經網絡控制策略。
首先選取吸氣式高超聲速飛行器的縱向動力學模型作為研究對象,基于反步控制設計框架,引入神經網絡,設計反步神經網絡控制器。為解決輸入受限問題,設計一種輔助系統對跟蹤誤差和理想控制律進行補償,保證控制輸出對參考軌跡的穩定跟蹤。最后,基于MATLAB仿真驗證了所設計控制策略的可行性與有效性。
2 模型描述
2.1 動力學建模
本文選取Parker針對吸氣式高超聲速飛行器提出的縱向平面運動模型[17]:
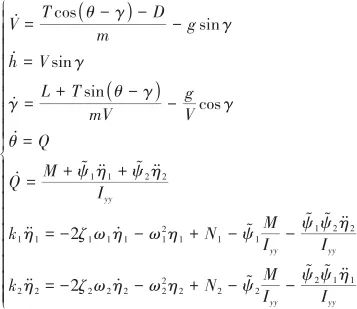 (1)
(1)
式中,V、h、γ、θ和Q這5個剛體狀態量分別代表高超聲速飛行器的速度、高度、航跡角、俯仰角和俯仰角速率;![]() 、
、![]() 、
、![]() 以及
以及![]() 分別代表飛行器的一、二階彈性模態及其導數;T、D、L和M分別為氣動力(推力、阻力及升力)和氣動力矩;
分別代表飛行器的一、二階彈性模態及其導數;T、D、L和M分別為氣動力(推力、阻力及升力)和氣動力矩;![]() 和
和![]() (i=1,2)分別為第i階彈性狀態量的阻尼系數和自然頻率;Ni(i=1,2)為第i階廣義彈性力;
(i=1,2)分別為第i階彈性狀態量的阻尼系數和自然頻率;Ni(i=1,2)為第i階廣義彈性力;![]() (i=1,2)為第i階彈性狀態量的耦合系數;k1和k2為常數;Iyy為y軸的轉動慣量;m為質量。為方便接下來的控制器設計,將氣動力和力矩分別改寫為仿射形式[17]:
(i=1,2)為第i階彈性狀態量的耦合系數;k1和k2為常數;Iyy為y軸的轉動慣量;m為質量。為方便接下來的控制器設計,將氣動力和力矩分別改寫為仿射形式[17]:
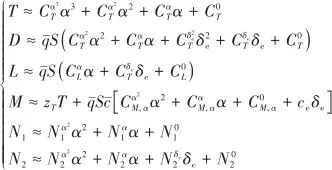 (2)
(2)
式中,![]() 為動壓,
為動壓,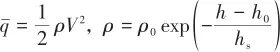 ;S和
;S和![]() 分別為參考面積和平均氣動弦長;
分別為參考面積和平均氣動弦長;![]() 為推力力臂;
為推力力臂;![]() 為攻角;
為攻角;![]() 為升降舵偏角;其余氣動參數分別為
為升降舵偏角;其余氣動參數分別為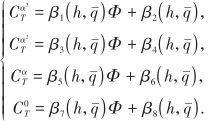
式中,![]() 為燃料當量比;
為燃料當量比;![]() 為第i階推力擬合參數。綜合式(1)和式(2)可得
為第i階推力擬合參數。綜合式(1)和式(2)可得
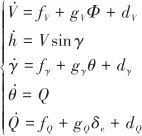 (3)
(3)
式中,![]()
![]()
![]()
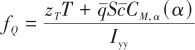
![]()
![]()
式中,![]() 、
、![]() 和
和![]() 均為包含彈性模態的不確定項。至此,完成了從式(1)的原理模型向面向控制模型式(3)的轉化。控制輸入分別為燃料當量比
均為包含彈性模態的不確定項。至此,完成了從式(1)的原理模型向面向控制模型式(3)的轉化。控制輸入分別為燃料當量比![]() 以及升降舵偏角
以及升降舵偏角![]() ,控制輸出為V、h。
,控制輸出為V、h。
2.2 神經網絡
為了避免模型中的不確定項對控制系統產生影響,這里引入徑向基神經網絡對其進行逼近:
![]() (4)
(4)
式中,![]() 和
和![]() 分別為神經網絡的輸入和輸出;
分別為神經網絡的輸入和輸出;![]() 為權值向量,
為權值向量,![]() ;
;![]() 為徑向基函數,
為徑向基函數,![]() 。典型的徑向基函數的形式為
。典型的徑向基函數的形式為
![]() (5)
(5)
式中,![]() 和
和 ![]() 分別為函數中心的向量大小以及寬度。假設
分別為函數中心的向量大小以及寬度。假設![]() 為一連續函數,存在一個理想的權值向量
為一連續函數,存在一個理想的權值向量![]() 使得下述等式成立[18]:
使得下述等式成立[18]:
![]() (6)
(6)
式中,![]() 為估計誤差;
為估計誤差;![]() 為估計誤差的上界。
為估計誤差的上界。
3 控制器設計![]()
為便于控制器設計,將式(3)拆分為速度和高度兩個子系統分別進行控制器設計。當然,這種設計思路只是在形式上加以區分,并不影響兩者間的耦合關系[19]。
3.1 速度控制器及穩定性證明
首先,將速度方程改寫為
![]() (7)
(7)
式中,FV為包含氣動力和力矩的函數,其表達式為![]()
定義速度的跟蹤誤差:
![]() (8)
(8)
為解決受限問題,引入一種新型輔助系統形式:
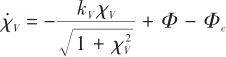 (9)
(9)
對式(7)修正可得
![]() (10)
(10)
對式(10)求導得
![]() (11)
(11)
為降低參數攝動、建模誤差對控制系統的影響,因此引入神經網絡對![]() 進行估計。其估計可表示為
進行估計。其估計可表示為
![]() (12)
(12)
式中,![]() 為權值向量
為權值向量![]() 的估計值。定義權值參數向量的最優值
的估計值。定義權值參數向量的最優值![]() 為
為
![]() (13)
(13)
則根據式(6)可將![]() 表示為
表示為
![]() (14)
(14)
式中,![]() 為逼近誤差,
為逼近誤差,![]() 為其上界。定義權值向量的估計誤差為
為其上界。定義權值向量的估計誤差為
![]() (15)
(15)
則有
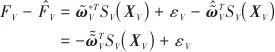 (16)
(16)
定義![]() 的自適應律為
的自適應律為
![]() (17)
(17)
式中,λV為正設計參數。構造速度子系統的可執行控制律為
![]() (18)
(18)
式中,![]() 、
、![]() 均為正的設計參數。將式(18)代入式(11)可得
均為正的設計參數。將式(18)代入式(11)可得
![]() (19)
(19)
選取速度子系統的Lyapunov函數為
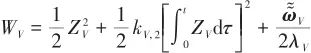 (20)
(20)
對式(20)求導得
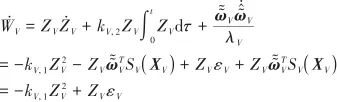 (21)
(21)
由于
![]() (22)
(22)
因此,式(21)可改寫為
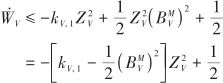 (23)
(23)
定義如下緊集:
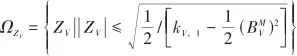 (24)
(24)
若![]() 不屬于集合
不屬于集合![]() ,且
,且![]() ,則有
,則有![]() 。
。
3.2 高度控制器及穩定性證明
為簡化高度控制系統設計,根據文獻[20]提出的方法構造高度h的控制律為
![]() (25)
(25)
式中,![]() 和
和![]() 均為待設計的正參數。令
均為待設計的正參數。令![]() ,即可實現h對
,即可實現h對![]() 的跟蹤[17]。在不考慮速度和高度方程的前提下,將式(3)改寫為
的跟蹤[17]。在不考慮速度和高度方程的前提下,將式(3)改寫為
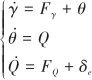 (26)
(26)
式中,![]()
![]()
與速度子系統類似,引入神經網絡對 ![]() 和
和![]() 估計:
估計:
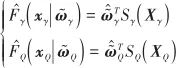 (27)
(27)
分別定義權值向量的最優值![]() 、
、![]() ,將
,將 ![]() 和
和![]() 表示為
表示為
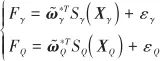 (28)
(28)
式中,![]() 和
和 ![]() 均為逼近誤差。定義
均為逼近誤差。定義![]() 和
和![]() 分別為
分別為![]() 和
和 ![]() 的上界。定義權值向量的估計誤差為
的上界。定義權值向量的估計誤差為
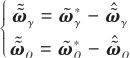 (29)
(29)
則有
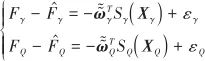 (30)
(30)
定義跟蹤誤差并求導得
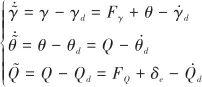 (31)
(31)
同樣,為解決受限問題,這里引入輔助系統形式對俯仰角速率進行補償:
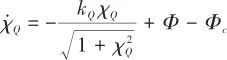 (32)
(32)
由于本文處理的是瞬時飽和,因此假定![]() 有界,其上界為
有界,其上界為![]() 。因此,式(32)可以改寫為
。因此,式(32)可以改寫為
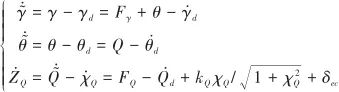 (33)
(33)
分別選取航跡角γ、航跡角θ和俯仰角速率Q的控制律為
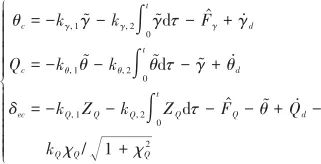 (34)
(34)
式中,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() 均為控制器參數。為避免出現反步系統中的“微分膨脹”問題,引入低通濾波器對中間控制量的導數求解:
均為控制器參數。為避免出現反步系統中的“微分膨脹”問題,引入低通濾波器對中間控制量的導數求解:
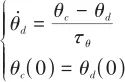 (35)
(35)
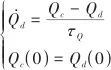 (36)
(36)
式中,![]() 和
和![]() 均為待設計的正參數。定義狀態量
均為待設計的正參數。定義狀態量![]() 和
和![]() 的估計誤差為
的估計誤差為
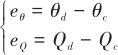 (37)
(37)
對式(37)求導得
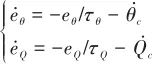 (38)
(38)
根據文獻[17]的結果可知:
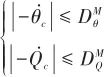 (39)
(39)
定義![]() 和
和![]() 的自適應估計律為
的自適應估計律為
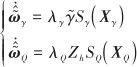 (40)
(40)
式中,![]() 、
、![]() 為正設計參數。選取高度子系統的Lyapunov函數為
為正設計參數。選取高度子系統的Lyapunov函數為
Wh=Wγ+Wθ+WQ(41)
式中,![]()
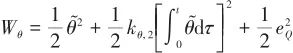
![]()
對式(41)求導得
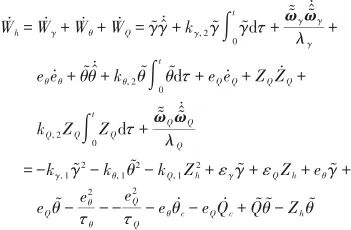 (42)
(42)
由于![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
則式(42)可改寫為
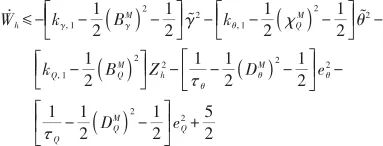 (43)
(43)
定義如下緊集:
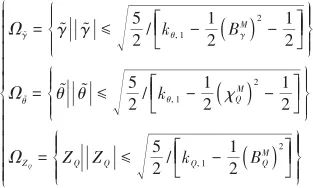 (44)
(44)
若上述誤差均位于式(44)中的緊集之外,同時控制參數符合下述關系式:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
則有![]() ,此時所有誤差信號均有界。
,此時所有誤差信號均有界。
4 仿真分析![]()
針對式(3)的模型進行閉環仿真,飛行器的初始取值如表1所示。
▼ 表1 初始狀態取值
▼ Tab. 1 Initial trim conditions
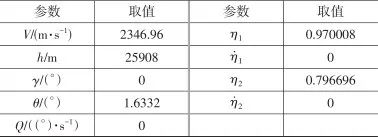
控制器參數為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;一階低通濾波器的設計參數為
;一階低通濾波器的設計參數為![]() ;輔助系統參數為
;輔助系統參數為![]() ,
,![]() ;彈性變量取值:
;彈性變量取值:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;神經網絡輸入:
;神經網絡輸入:![]() ,
,![]() ,
,![]() ;輸入區間定義為
;輸入區間定義為![]() ,
,![]() ,
,![]() ,
,![]() ;徑向基函數的參數
;徑向基函數的參數![]() ,
,![]() ,
,![]() ,
,![]() 。為了驗證控制器效果,將控制輸入的約束范圍設定為
。為了驗證控制器效果,將控制輸入的約束范圍設定為![]() ,
,![]() 。為了檢驗系統的魯棒性,在
。為了檢驗系統的魯棒性,在![]() 時分別向動力學模型中加入下列擾動:
時分別向動力學模型中加入下列擾動:![]() ,
, ![]() 。定義速度階躍
。定義速度階躍![]() ,高度階躍
,高度階躍![]() 。控制系統的輸入的仿真結果如圖 1~圖4所示。圖1為對控制律和跟蹤誤差進行補償情況下,燃料當量比
。控制系統的輸入的仿真結果如圖 1~圖4所示。圖1為對控制律和跟蹤誤差進行補償情況下,燃料當量比![]() 及其輔助系統曲線。由圖1可以看出,大約在30~50 s的仿真時間內
及其輔助系統曲線。由圖1可以看出,大約在30~50 s的仿真時間內![]() 出現了飽和,此時輔助系統能夠迅速響應進行補償,使得控制輸入盡快退出飽和狀態。作為對比,圖2所示為無補償的情況,可以看出
出現了飽和,此時輔助系統能夠迅速響應進行補償,使得控制輸入盡快退出飽和狀態。作為對比,圖2所示為無補償的情況,可以看出![]() 出現了持續的飽和,控制律失效直至仿真終止。圖3所示為有補償情況下升降舵偏角
出現了持續的飽和,控制律失效直至仿真終止。圖3所示為有補償情況下升降舵偏角![]() 及其輔助系統的輸出曲線,可以看出
及其輔助系統的輸出曲線,可以看出![]() 在仿真初期雖然出現了短暫的受限,但由于有輔助系統的存在,其很快恢復到正常狀態。圖4所示為無補償的狀態,此時由于
在仿真初期雖然出現了短暫的受限,但由于有輔助系統的存在,其很快恢復到正常狀態。圖4所示為無補償的狀態,此時由于![]() 出現了持續飽和,控制律失效導致控制失敗。
出現了持續飽和,控制律失效導致控制失敗。
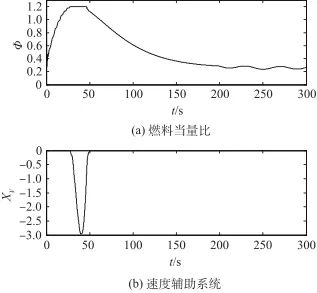
▲ 圖1 燃料當量比及其輔助系統曲線(有補償)
▲ Fig.1 Curves of fuel equivalent ratio and auxiliary system(with compensation)
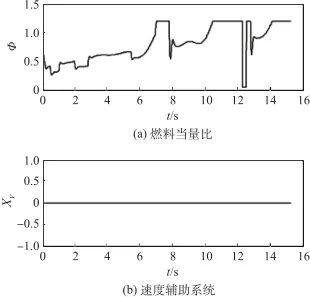
▲ 圖2 燃料當量比及其輔助系統曲線(無補償)
▲ Fig.2 Curves of fuel equivalent ratio and auxiliary system(without compensation)
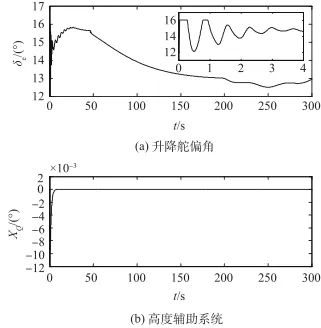
▲ 圖3 升降舵偏角及其輔助系統曲線(有補償)
▲ Fig.3 Curves of elevator deflection angle and auxiliary system(with compensation)
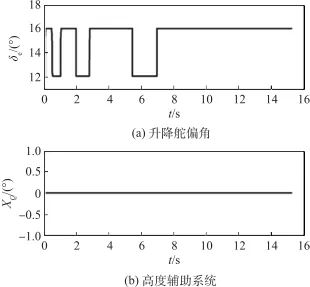
▲ 圖4 升降舵偏角及其輔助系統曲線(無補償)
▲ Fig.4 Curves of elevator deflection angle and auxiliary system(without compensation)
控制系統的速度和高度輸出及其各自的跟蹤誤差如圖5~圖8所示。與前面類似,分別將有補償和無補償的情況做一對比。從仿真結果可以看出,有補償時,速度和高度都能穩定跟蹤各自的參考軌跡,調節時間很短。如果去除補償策略,速度和高度則無法跟蹤參考軌跡,控制失敗。
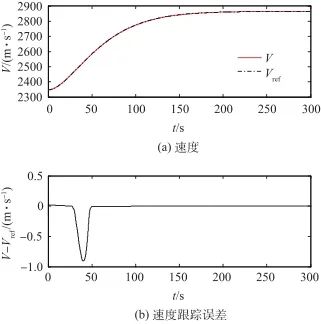
▲ 圖5 速度及其跟蹤誤差曲線(有補償)
▲ Fig.5 Curves of velocity and tracking error(with compensation)
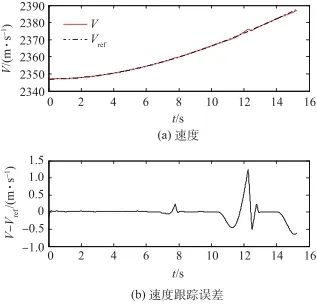
▲ 圖6 速度及其跟蹤誤差曲線(無補償)
▲ Fig.6 Curves of velocity and tracking error(without compensation)
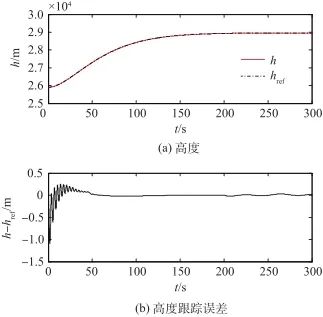
▲ 圖7 高度及其跟蹤誤差曲線(有補償)
▲ Fig.7 Curves of altitude and tracking error(with compensation)
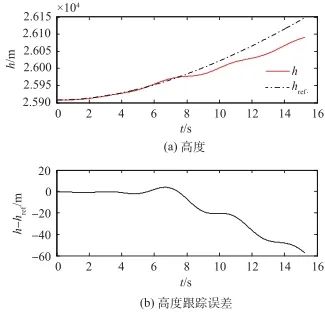
▲ 圖8 高度及其跟蹤誤差曲線(無補償)
▲ Fig.8 Curves of altitude and tracking error(without compensation)
5 結 論
(1)本文針對輸入受限條件下的高超聲速飛行器精確穩定跟蹤控制策略開展研究。通過構造一種新型輔助系統,在控制輸入受限時能夠繼續執行控制律。仿真結果表明,當控制輸入的幅值出現持續飽和時,所設計的輔助系統能夠及時對跟蹤誤差與控制律進行補償,使得控制輸入退出飽和狀態,恢復對參考軌跡的持續跟蹤,確保飛行器的飛行姿態穩定。
(2)不同于文獻[16]中基于精確數學模型構造控制器,即將模型不確定性歸為干擾項,利用干擾觀測器對不確定項進行逼近的思路。本文將模型中包含氣動力在內的各種作用力及不確定項歸結為總的非線性未知函數,引入神經網絡對其估計,進一步弱化了控制器對模型的依賴。從仿真結果可以看出,速度與高度的跟蹤誤差超調量及調節時間均非常小,獲得了較為滿意的控制性能。
(3)本文雖然對輸入受限問題的研究主要集中于對幅值飽和的補償,而對控制量帶寬與速率的受限問題未作考慮。因此,下一步對幅值、帶寬和速率同時受限問題開展相關研究是將輸入受限問題推廣到實際應用中必須開展的工作。
編輯:黃飛
 電子發燒友App
電子發燒友App






















評論